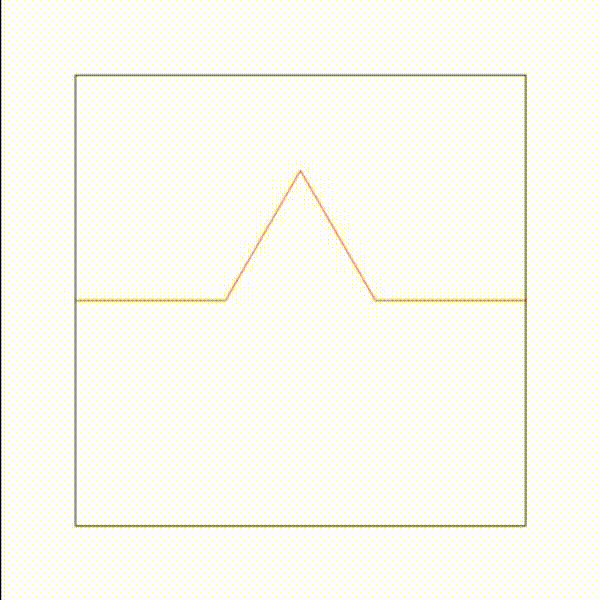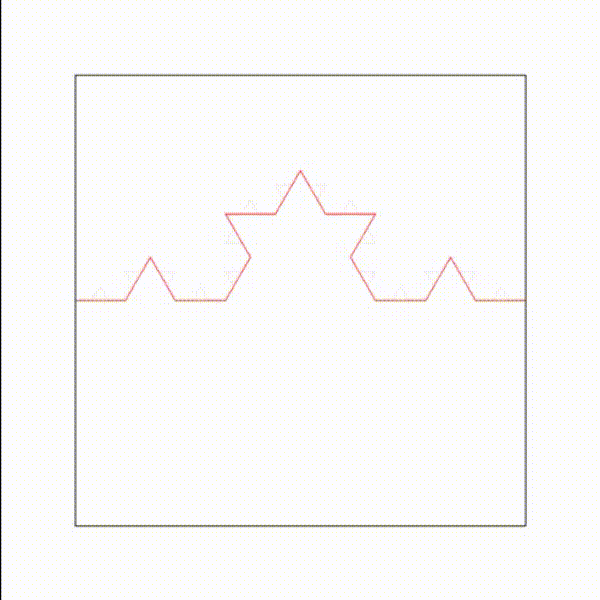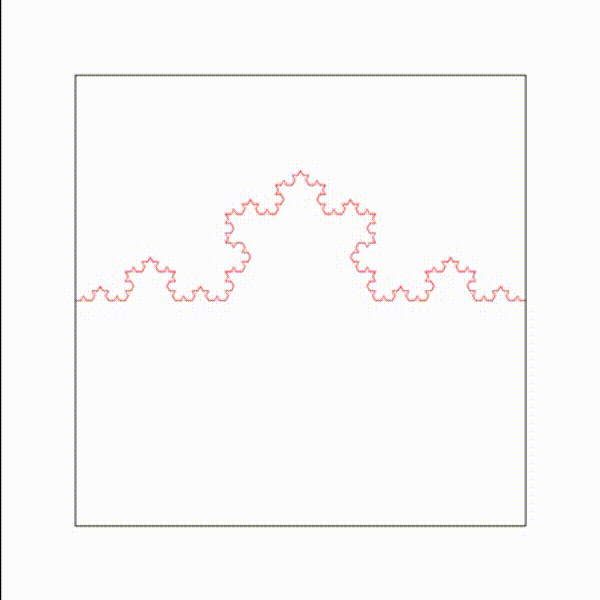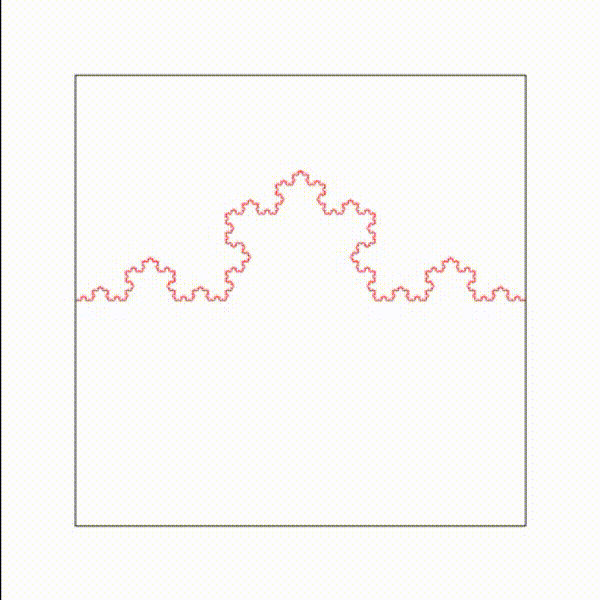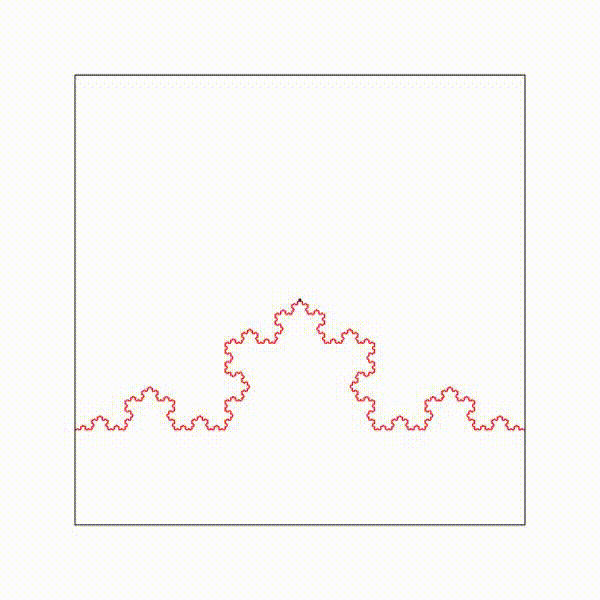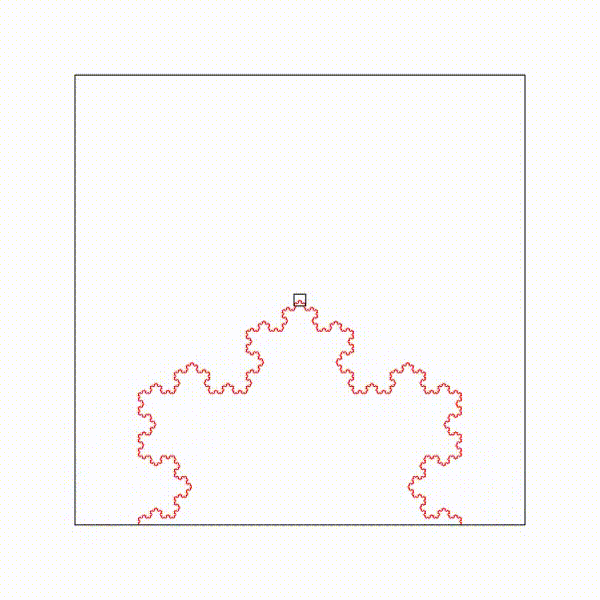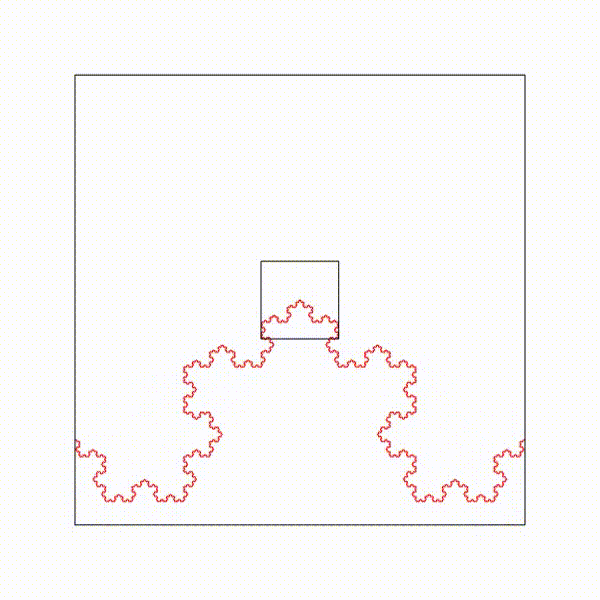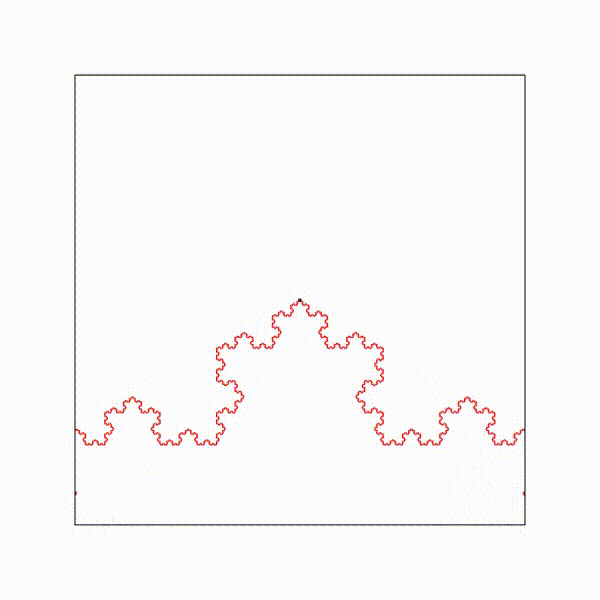
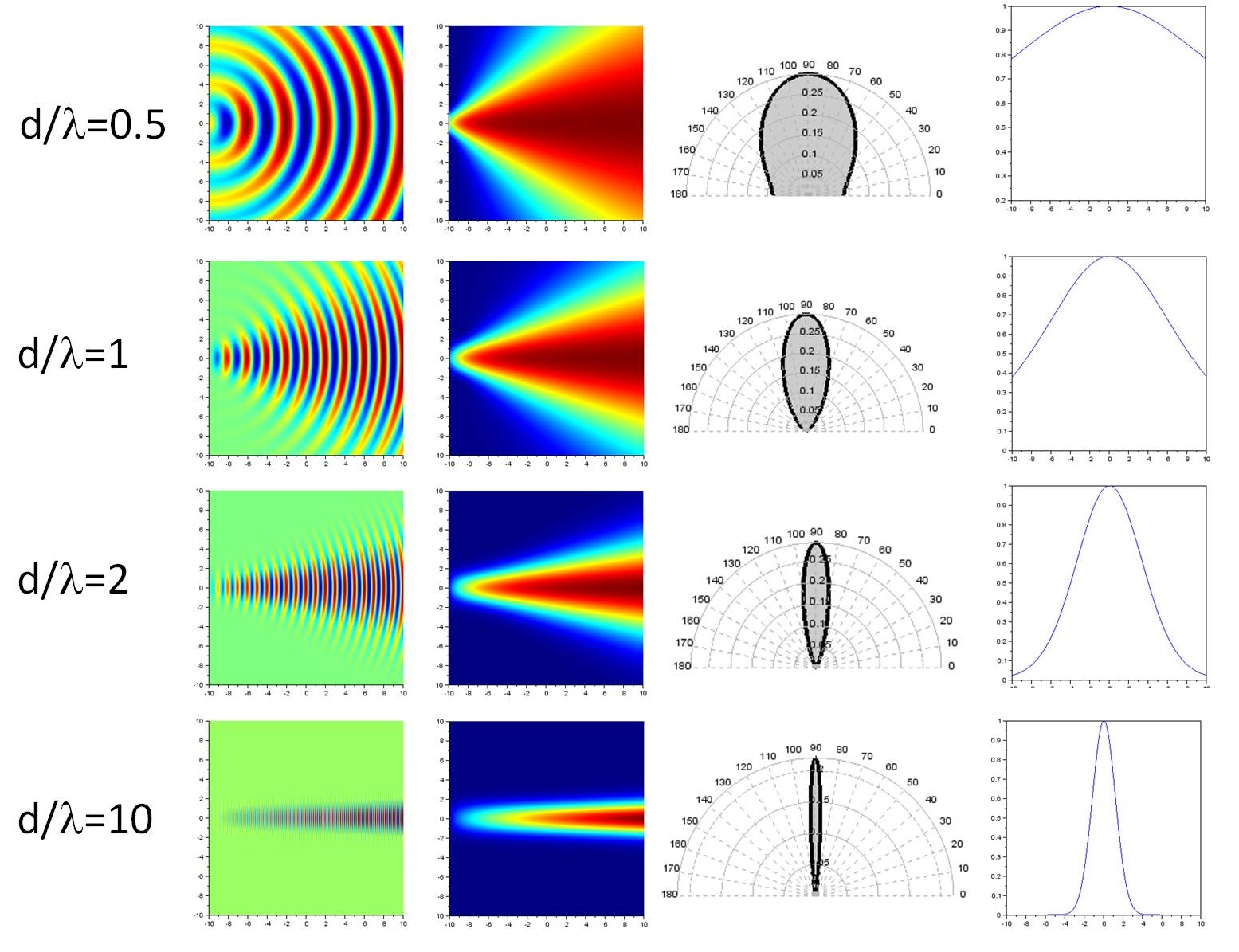
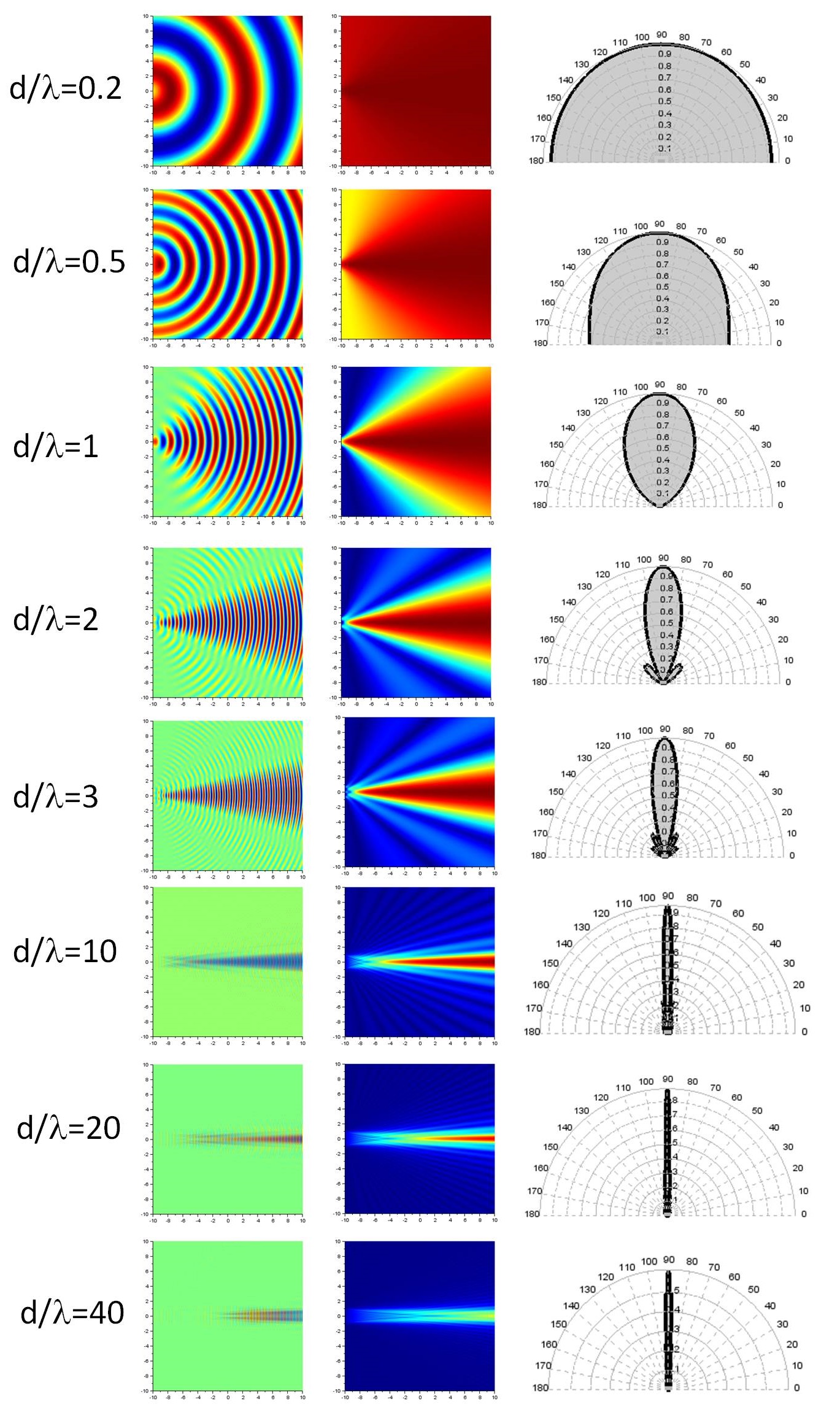
Illustration de la diffraction, valable en acoustique et en optique. Une onde de longueur d'onde lambda qui traverse un diaphragme de diamètre d est diffractée, lorsque d est du même ordre de grandeur que lambda. Le phénomène de diffraction est analogue à la génération du rayonnement acoustique par un piston circulaire de diamètre d, où chaque point de la surface du piston émet des ondes sphériques de longueur d'onde lambda (principe de Huyguens-Fresnel). La première colonne montre l'amplitude de l'onde. La deuxième colonne montre l'intensité de l'onde. La troisième colonne montre un diagramme de directivité : intensité en fonction de l'angle par rapport à l'axe. Lorsque d/lambda est faible, c'est-à-dire lorsque la longueur d'onde est grande devant la taille de l'émetteur, il s'agit d'une source ponctuelle. Le rayonnement est uniforme quelque soit la direction, on dit qu'il est isotrope. Cependant on constate que la directivité dépend de la longueur d'onde : plus la fréquence est haute, plus le faisceau est directif. Cela signifie que les basses fréquences diffractent plus que les hautes fréquences. La diffraction se comporte donc comme un filtre passe-bas, dont la fréquence de coupure diminue lorsque la distance à l'axe augmente. De plus on note l'apparition de lobes secondaires dans la fonction de directivité. Proche du piston, la distribution en intensité est compliquée. C'est le champ proche, ou zone de Fresnel. Loin du piston, le faisceau diverge avec un angle gamma. C'est le champ lointain, ou zone de Fraunhofer. La transition entre champ proche et champ lointain se trouve à une distance z=(d/2)²/lambda. En champ lointain, l'intensité est la transformée de Fourier de la distribution d'amplitude au niveau du piston. Dans le domaine de l'optique,on appelle cela l'optique de Fourier. Dans le cas d'une fente, la distribution d'intensité sera proportionnelle à un sinus cardinal carré sinc². Dans le cas d'un trou, la distribution sera une tache d'Airy, qui s'exprime avec des fonctions de Bessel du premier ordre J1.

Illustration de la diffraction par un faisceau gaussien. Le piston cylindrique émet un rayonnement acoustique, avec une distribution gaussienne. Rappelons qu'une fonction gaussienne est une fonction "en cloche" de la forme f(x)=A*exp(-x^2/(2*a^2)). Cette fonction ne s'annule jamais, ce qui signifie qu'elle a théoriquement une extension illimitée. On constate que la distribution du faisceau en intensité reste toujours gaussienne, c'est la particularité des faisceaux lasers, qui obéissent à l'optique gaussienne. Dans le cadre de l'optique de Fourier, cela provient du fait que la transformée de Fourier d'une gaussienne est aussi une gaussienne. La longueur de Rayleigh est donc formellement identique à la limite de champ proche.

Retour sur la page d'accueil - Retour en haut de page